三维曲线方程的描述是数学中研究曲线在三维空间中的表示和性质的一个重要课题。三维曲线可以描述空间中的各种形状,包括直线、曲线、螺旋线等。为了描述这些曲线,数学家发展了一种基于参数方程的方法,通过引入参数来描述曲线上的每一个点的位置。

三维曲线可以用参数方程表示为:
x = f(t)
y = g(t)
z = h(t)
其中t是参数,f(t),g(t),h(t)是关于t的函数。这三个函数决定了曲线在三维空间中的形状。通过选择不同的函数,我们可以得到各种不同类型的曲线。
一种常见的三维曲线是直线。直线可以用参数方程表示为:
x = a + bt
y = c + dt
z = e + ft
其中a,b,c,d,e,f是常数,代表直线在三维空间中的位置和方向。通过调整这些常数,我们可以得到不同位置和方向的直线。
除了直线,还有许多其他类型的三维曲线。例如,圆弧可以用参数方程表示为:
x = rcos(t)
y = rsin(t)
z = h(t)
其中r是半径,t是参数,h(t)是关于t的函数。这个参数方程描述了一个在平面上旋转的圆弧。
另一个有趣的例子是螺旋线。螺旋线可以用参数方程表示为:
x = rcos(t)
y = rsin(t)
z = ht
其中r是螺旋线的半径,h是螺旋线沿着z轴方向的变化速率,t是参数。这个参数方程描述了一个沿着z轴螺旋上升的曲线。
三维曲线的参数方程可以用来描述曲线的形状、方向和大小。通过改变参数方程中的参数,我们可以对三维曲线进行变换。例如,改变参数的范围可以改变曲线的长度。调整参数方程中的参数可以改变曲线的形状,使其变得更弯曲或更直。通过变换参数方程中的常数,我们可以将曲线平移或旋转到不同的位置和方向。
通过研究三维曲线的参数方程,我们可以深入了解曲线的性质和行为。我们可以计算曲线的切线和法线,研究曲线在不同点的斜率和曲率。我们还可以计算曲线的长度和弧长,研究曲线的弯曲程度。这些性质对于理解和应用三维曲线都非常重要。
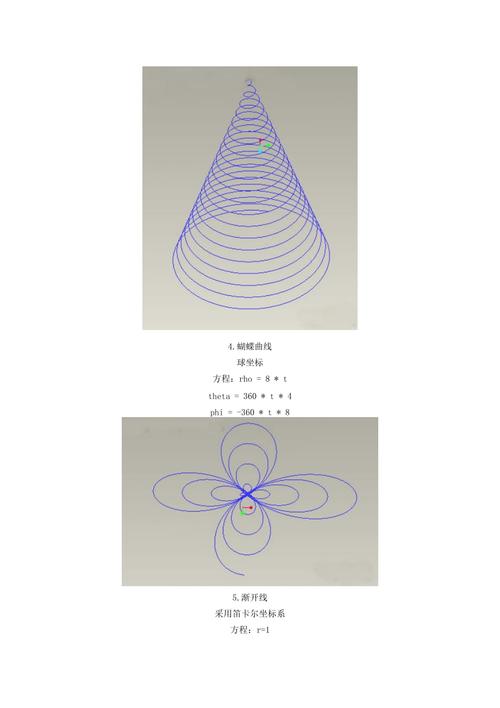
总之,三维曲线方程的描述是数学中研究曲线在三维空间中的表示和性质的一个重要课题。通过参数方程,我们可以描述和变换各种不同类型的曲线。研究三维曲线的参数方程可以揭示曲线的性质和行为,为数学研究和实际应用提供了重要的工具和方法。
转载请注明来源本文地址:https://www.tuituisoft/blog/21066.html