在几何学中，五边形是一个具有五个边的多边形。它是多边形中较为特殊的一个，因为它具有许多独特的特征和性质。然而，创建一个精确的五边形有时可能会有一些挑战。但是，幸运的是，我们有一种被称为"Dynamo的五边形创建方法"的技术，可以帮助我们轻松地构造出一个完美的五边形。接下来，我们将深入探讨这个方法的具体步骤和原理。

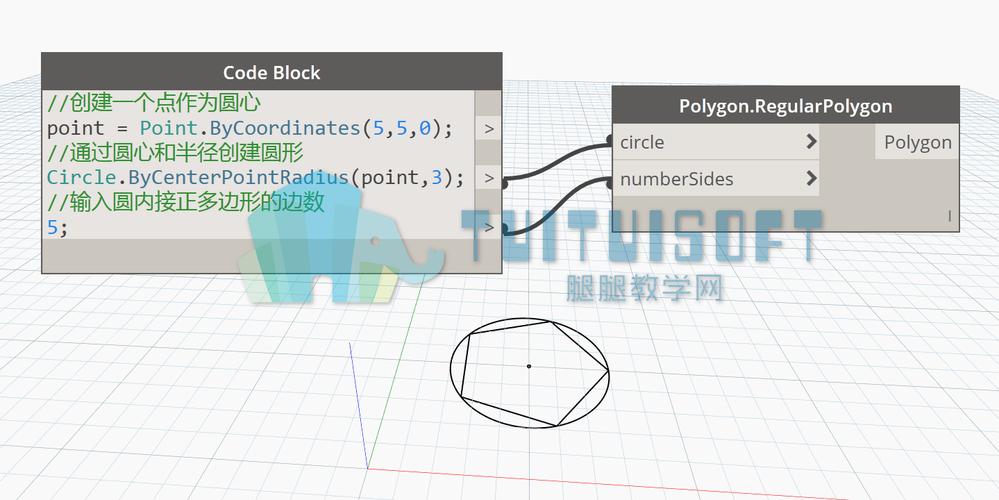
"Dynamo的五边形创建方法"是以17世纪的著名数学家Peter Friedrich Ludwig Dirichlet的名字命名的。该方法利用了数学中的一些基本原理和性质，其中一个关键原理是黄金分割比例。黄金分割比例是指将一条线段分为两部分，使整条线段与较长部分的比值等于较长部分与较短部分的比值。这个比例约为1.6180339887。

现在，我们将开始介绍"Dynamo的五边形创建方法"的步骤。首先，我们需要绘制一个正三角形。然后，我们需要找到三角形的中点，并将其与一个边的顶点连接起来。接下来，我们需要找到这条线段的中点，并将其与正三角形的底边上的两个顶点连接起来。现在，我们已经得到了一个更小的正三角形和一个线段。我们需要重复这个过程，每次都将线段连接到前一个正三角形的底边上的两个顶点，直到我们得到一个小到足以构成五边形的正三角形。

现在，让我们来揭示"Dynamo的五边形创建方法"的原理。在创建过程中，我们每次都将前一个正三角形的底边的两个顶点与线段连接起来。这些线段的长度将呈现出一个特殊的关系，即它们按照黄金分割比例递增。这就是为什么我们能够通过绘制连续的正三角形来构建一个完美的五边形的原因。此外，这种方法还利用了正三角形的性质，即它的内角和为180度。因此，通过绘制连续的正三角形，我们能够得到一个五边形，其内角和为540度，符合几何学中五边形的定义。

通过"Dynamo的五边形创建方法"，我们不仅可以构建一个完美的五边形，还可以进一步研究五边形的性质和特征。例如，我们可以观察到五边形的对角线之间存在多种关系，并探索其对称性和对角线的长度比例。我们还可以研究五边形的边和顶点之间的关系，并了解它们之间的数学性质和几何特征。此外，通过"Dynamo的五边形创建方法"，我们还可以进一步研究黄金分割比例及其在几何学中的应用。

总之，"Dynamo的五边形创建方法"是一个在几何学中构建五边形的有效技术。通过利用黄金分割比例和正三角形的性质，我们能够轻松地构造出一个完美的五边形。这种方法不仅可以帮助我们创建五边形，还可以进一步研究五边形的性质和特征。无论是在学术研究还是实际应用中，"Dynamo的五边形创建方法"都具有重要的意义和价值。

转载请注明来源本文地址：https://www.tuituisoft/blog/21000.html