计算三维曲线的长度是数学中的一个重要问题。三维曲线的长度是指曲线上各点之间的距离总和。在计算三维曲线长度时，我们可以利用微积分中的曲线积分来解决。

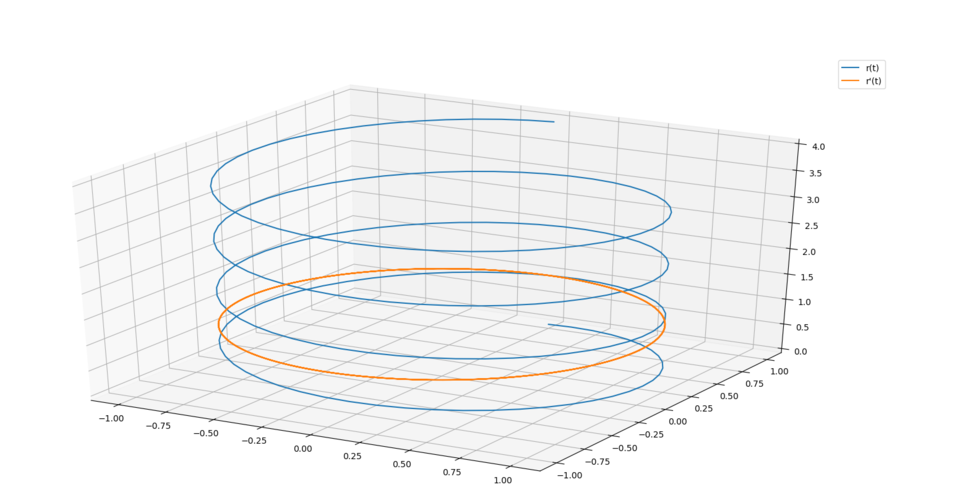
首先，我们需要将三维曲线参数化。参数化是指通过一个或多个参数来表示曲线上的点。常见的参数化方法有向量值函数和参数方程。

对于向量值函数表示的曲线，我们可以将曲线定义为一个向量函数r(t)，其中t是参数。例如，我们可以将曲线表示为r(t) = (x(t), y(t), z(t))。然后，我们可以将曲线长度的计算问题转化为对r(t)的积分问题。

对于参数方程表示的曲线，我们可以将曲线定义为三个关于参数t的函数x(t)，y(t)和z(t)。然后，我们可以将曲线长度的计算问题转化为对x(t)，y(t)和z(t)的积分问题。

对于向量值函数的曲线，我们可以使用以下公式来计算曲线的长度：

L = ∫_a^b ||r'(t)|| dt

其中，L是曲线的长度，r'(t)是r(t)的导数，||r'(t)||是向量r'(t)的模，a和b是参数的起始值和结束值。

对于参数方程的曲线，我们可以使用以下公式来计算曲线的长度：

L = ∫_a^b √[(x'(t))² + (y'(t))² + (z'(t))²] dt

其中，L是曲线的长度，x'(t)，y'(t)和z'(t)分别是x(t)，y(t)和z(t)的导数，a和b是参数的起始值和结束值。

通过对曲线参数化并应用上述公式，我们可以计算出三维曲线的长度。这对于很多应用领域都非常重要，例如计算机图形学、物理学和工程学等。

总之，计算三维曲线的长度是一个重要的数学问题。我们可以通过将曲线参数化并应用曲线积分的方法来解决这个问题。通过计算曲线长度，我们可以在各种应用领域中更好地理解和分析曲线的性质和行为。

转载请注明来源本文地址：https://www.tuituisoft/blog/21054.html