三维曲线是指在三维空间中由一系列点构成的连续曲线。它是通过在三维坐标系中的不同点之间描绘连续的路径而形成的。

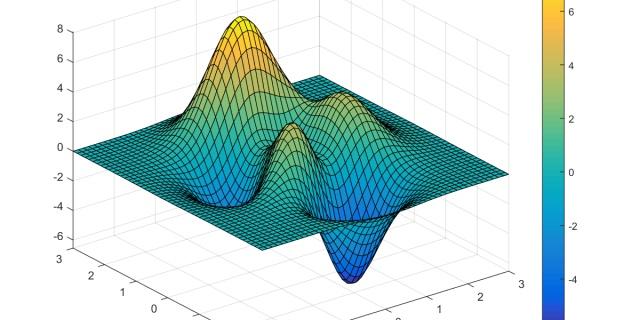
三维曲线可以用于描述现实世界中的各种物理、几何和数学现象。在物理学中，三维曲线可以表示物体在空间中的运动轨迹。在几何学中，三维曲线可以用来表示各种曲线形状和曲面的交线。在数学中，三维曲线是多元函数的图形表示。

三维曲线是通过在三维空间中的点之间绘制线段来形成的。这些点可以代表空间中的对象的位置，例如运动物体的位置或几何图形上的点。通过在这些点之间绘制线段，我们可以看到曲线所代表的路径。

三维曲线具有一些特殊性质，比如曲率和曲率半径。曲率是描述曲线弯曲程度的量度，它表示曲线在给定点处相对于该点的弯曲程度。曲率半径则是描述曲线弯曲程度大小的数量。通过计算这些特殊性质，我们可以进一步了解曲线的形状和性质。

三维曲线还可以用来表示空间中的路径和轨迹。例如，地球上的飞行器在飞行时会遵循一条特定的三维曲线，这条曲线描述了飞行器在空间中的路径。通过研究飞行器的三维曲线，我们可以了解飞行器的航行路径和轨迹。

此外，在数学上，三维曲线是多元函数的图形表示。多元函数是具有多个自变量和一个因变量的函数。通过绘制三维曲线，我们可以可视化多元函数的图像，从而更好地理解函数的性质和行为。

总之，三维曲线是在三维空间中由一系列点构成的连续曲线。它可以用来描述现实世界中的各种物理、几何和数学现象。通过研究三维曲线的形状和特性，我们可以更深入地理解曲线所代表的对象的位置、路径和行为。

转载请注明来源本文地址：https://www.tuituisoft/blog/21061.html